- 2022-11-18

5重勝単勝馬券
WIN5(ウィンファイブ)とは、JRAの発売する勝馬投票券の一種で「5つの指定されたレースの1着馬をすべて当てるもの」。JRA発売の勝馬投票券の中では最も難易度が高く、したがって払戻金も高額になることが魅力である。規定上の最大の払戻金額は「100円に対して6億円」であるが、未だに出現していない。
WIN5の歴史
始まり
2011年4月24日の皐月賞開催日から発売が開始された。その結果は、単勝人気順(1-3-3-3-4)で的中票数663票、配当金額は810,280円だった。
経過
2022年11月13日まで650回が実施され、中止・不成立が12回、的中なしが7回となっている。
配当金
最高配当は、554,446,060円(4-4-10-8-3)で、配当金1億円以上は36回。
最低配当は、6,050円(1-1-2-2-1)で、配当金10万円以下は52回。
平均配当は、19,961,979円(同着4回を含む)。
WIN5の買い方
対象レース
原則として、「各競馬場メインレースのなかで発走時刻が最も遅いレースからさかのぼって5レースを指定」。ただし、季節によっては原則から外れる場合がある。(夏場の開催など)
発売方法
インターネット投票(即PAT、A-PAT、JRAダイレクト)およびUMACA投票(UMACAシート)により1投票100円単位で発売する。
締切時間
指定された最初のレースの発走予定時刻の5分前(JRAダイレクトは10分前)
WIN5の配当金計算方法
配当金額の計算
WIN5の配当金額は以下の計算式で決定される。
(総払戻金額)=(売上金額)x0.70+(前回のキャリーオーバー金額)
(配当金額)=(総払戻金額)÷(的中組合せ数(*1))÷(的中票数)
(*1)指定レースで1着同着があった場合に2以上になる
キャリーオーバー
配当金額の上限は6億円(2014年6月6日以前は2億円)でそれを超えた部分はキャリーオーバーとして次回に持ち越しとなる。的中票数が0の場合は、総払戻金額の全額がキャリーオーバーとなる。
キャリーオーバーがある場合の実績
| 実施年月日 | 総売上票数 | 的中票数 | 配当金額 | CO事由 |
|---|---|---|---|---|
| 2011/07/03 | 22,630,035 | 108,638 | 19,680 | 配当上限 |
| 2011/09/11 | 28,327,503 | 2,920 | 1,008,010 | 的中なし |
| 2012/12/02 | 12,737,437 | 299 | 3,978,890 | 配当上限 |
| 2012/12/16 | 11,541,735 | 11 | 86,610,770 | 配当上限 |
| 2013/05/12 | 17,047,103 | 15,730 | 114,070 | 的中なし |
| 2013/10/13 | 10,820,356 | 2,814 | 418,200 | 配当上限 |
| 2014/03/09 | 11,293,956 | 438 | 2,456,090 | 配当上限 |
| 2014/03/23 | 9,758,649 | 11,075 | 74,650 | 配当上限 |
| 2014/09/14 | 15,797,446 | 1,223 | 1,238,270 | 的中なし |
| 2014/11/24 | 11,496,896 | 789 | 1,541,710 | 的中なし |
| 2018/12/28 | 34,993,422 | 115,874 | 29,330 | 的中なし |
| 2019/03/10 | 23,028,848 | 749 | 10,282,010 | 的中なし |
| 2020/07/26 | 33,813,341 | 3,274 | 816,800 | 的中なし |
2014年6月に配当上限が6億円に引き上げられてからは、配当上限によるキャリーオーバーは出ていないがそれ以前では6回あった。
一方、的中なしによるキャリーオーバーは7回ありいずれも総売上票数が大幅に増加している。これまでのWIN5の総売上金額の1位から7位までをキャリーオーバー回が占めており、2018年12月28日の約35億円が歴代1位である。
WIN5のオッズ
JRA公式情報
WIN5の投票は、買い目が通常10万通り以上あることから、買い目ごとのオッズは提供されず、各対象レース終了後にそれまでの的中票数のみが発表される。
WIN5オッズ推定方法
WIN5の買い目ごとの配当額を予想する手法は2種類あり、いずれも単勝オッズを利用した計算方法である。原則は「個々の出走馬の単勝馬券の売上げ比率とWIN5における当該馬を含んだ組合せの売上げ比率はほぼ等しい」という仮説を前提に「WIN5における組合せの票数比率を各レースにおける選択馬の単勝売上比率の積とする」方法である。
この仮説を検証するためにWIN5各レースを対象に「1着馬の単勝売上比率とWIN5における売上比率」の分布図を作成した。
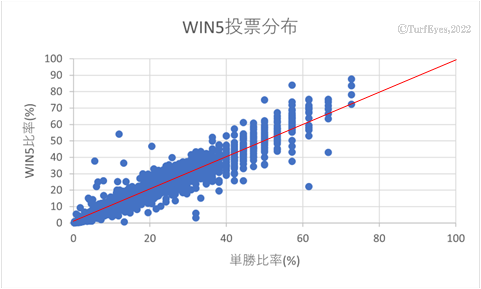
この分布図はWIN5売上比率のデータが1着馬以外は発表されないため1着馬のみを対象にしているが、1着馬以外の各馬に関しても事前に1着馬がわかるわけではないので異なる分布を示す理由はない。したがって、この分布が母集団の分布に近いと考えて良いだろう。ばらつきはあるものの、ほぼ1対1の比例関係(赤線)とみて良いだろう。
結果として、「個々の出走馬の単勝馬券の売上げ比率とWIN5における当該馬を含んだ組合せの売上げ比率はほぼ等しい」という仮説は成立すると言える。
WIN5オッズの理論値
(1) 各レースの指定馬の単勝オッズをr1、r2、r3、r4、r5とし、これらの積をX(=r1xr2xr3xr4xr5)とする
(2) 各レースにおける該当馬の単勝票数比率は、0.8/r1、0.8/r2、0.8/r3、0.8/r4、0.8/r5
(3) Win5の指定買い目の票数比率をRとすると前項の前提から
R=(0.8/r1)(0.8/r2)(0.8/r3)(0.8/r4)(0.8/r5)=0.8^5/(r1xr2xr3xr4xr5)=0.262144/X
(4) Win5理論値オッズをPmとすると
Pm=70/R=70/0.262144xX=267X
(5) 従って、「WIN5理論値オッズは、各選択馬の単勝オッズの積の267倍である」
WIN5オッズの統計値
前項の式の精度を検証するため、WIN5配当金額をPrとし、オッズ係数Pr/Xの値を集計した結果を以下に示す。
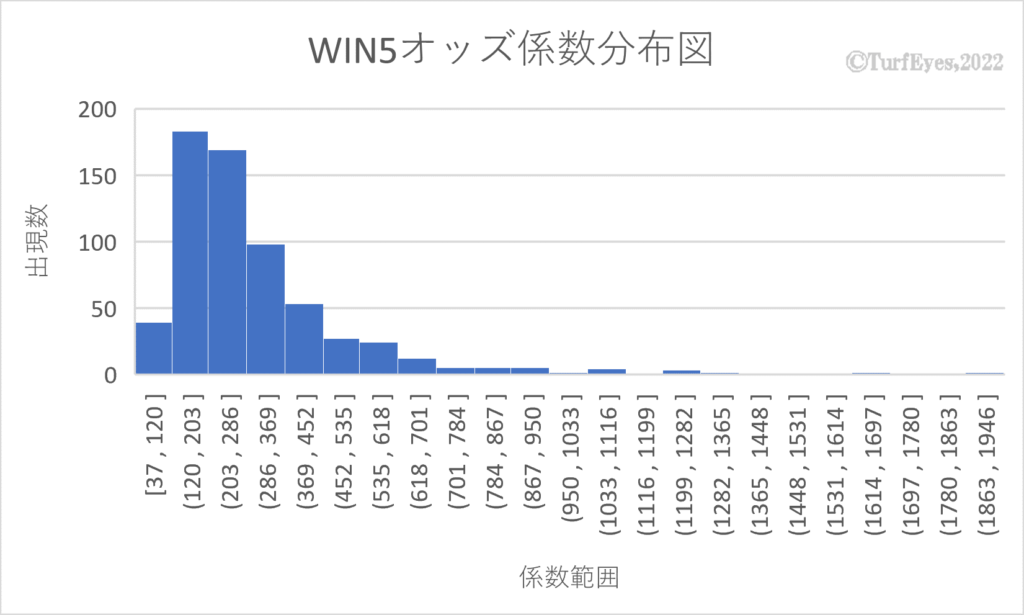
(最高値)=1904 (配当2億円、票数1、単勝オッズ:3.4-41.5-16.1-6.8-6.8)
(最低値)=37 (配当45,313,190円、票数10、単勝オッズ:19.5-24.5-11.9-11-19.5)
(平均値)=299 (中央値)=243
最低値の配当が非常に高く意外に思われるが、的中票数が少ない(単勝オッズが高い)場合は前提となる比例条件の誤差が大きくなるため偶然性に大きく左右されるということであろう。しかしそれにしても5レース全てが単勝10倍以上で決まっているのに的中票が10票あることが驚異的といえる。
結論として平均値を採用すると、「WIN5統計値オッズは、各選択馬の単勝オッズの積の299倍である」
WIN5の方法論
全点買い
よくある質問に「WIN5を全点買いしたら儲かるか?」というものがあるが、ほとんどの回で買い目は10万通りから最大で約189万通りあるので、統計的にはNOであるが、毎回数千万円を賭ける財力と強運があれば破産する前に大当たりするかもしれないのであながち全否定はできない。
1点買い
反対に「毎回1点のみで賭けたらどうなるか?」のほうが現実的に面白いので検討の価値は高い。
(1) もっとも初歩的な例で、「全て1番人気馬を選択する」というアプローチの結果は・・・
(購入票数)638 (的中回数)1 (総配当金額)10,260円 (回収率)16%
(2) 「全て2番人気馬を選択する」というアプローチの結果は・・・全滅
(3) 以下ゾロ目人気の1点買いは全て不発
一般的に1番人気馬の勝率は約1/3ほどなので、単純に考えると「3の5乗分の1」で約0.4%の的中率が期待されるが638回の試行で的中1回は低すぎる気もするが・・・
2番人気以降の勝率は1番人気馬に比べるとぐっと低くなるので全滅は統計的にわかりやすい。
範囲買い
さすがに「WIN5は1点では的中は難しい」ということで買い目の範囲を広げ、現実的に的中が期待できる買い方を検討する。そこで、上位人気馬を数頭の範囲で組み合わせた方法で試行するが果たして収支は・・・
(1) 1番人気馬と2番人気馬の組み合わせ32点買いの場合
(購入票数)32×638=20,416 (的中回数)23 (総配当金額)1,393,460円 (回収率)68%
(2) 1番人気馬と2番人気馬と3番人気馬の組み合わせ243点買いの場合
(購入票数)243×638=155,034 (的中回数)58 (総配当金額)9,185,940円 (回収率)59%
(3) 1番人気馬から4番人気馬までの全組み合わせ1,024点買いの場合
(購入票数)1,024×638=653,312 (的中回数)107 (総配当金額)42,749,910円 (回収率)65%
(1)の回収率は、WIN5の払戻率70%と大差なく、的中回数も多く買い目もそれほど多くないので、利益は期待できないが入門用としては面白い。
(2)(3)では、買い目が多く、それに伴い的中回数も多くなるが回収率は良くなく、損失も大きい。これは人気サイドの選択なので配当が安いことが原因。したがって、人気サイドで網羅的に買うのはお勧めできない。
フォーメーション買い
前項の結果から、1番人気馬から4番人気馬の範囲では配当が安く回収率が上がらないことが判明したので5番人気以降にも選択肢を広げることにする。範囲で網羅すると買い目が膨大になるのでフォーメーションを分割して買い目数を抑える。ただし、JRAのインターネット投票では一括で指定できない買い方なので買い目毎に入力が必要になる。
(1) 1番人気馬を4レースと4番人気馬を1レース選択
(買い目数)5(4番人気馬を買うレースの選択肢は5通り)
(購入票数)5×638=3,190 (的中回数)3 (総配当金額)433,110円 (回収率)136%
(2) 1番人気馬を4レースと5番人気馬を1レース選択
(買い目数)5(5番人気馬を買うレースの選択肢は5通り)
(購入票数)5×638=3,190 (的中回数)4 (総配当金額)700,230円 (回収率)220%
(3) 1番人気馬を4レースと6番人気馬を1レース選択
(買い目数)5(5番人気馬を買うレースの選択肢は5通り)
(購入票数)5×638=3,190 (的中回数)0 (総配当金額)0円 (回収率)0%
競馬の知識が無くてもWIN5で勝てる投票法:1×4(One by Four)
前項の結果から、1番人気馬を4レース、4~6番人気馬を1レース選択する方法では、回収率がそれぞれ136%、220%、0%となった。おそらく5番人気馬と6番人気馬の落差は統計的な偏りなので、それを考慮して(1)(2)(3)の投票法を並行的に実施すると以下の結果になる。
(購入票数)5x3x638=9,570 (的中回数)7 (総配当金額)1,133,340円 (回収率)118%
この人気薄1頭と1番人気馬4頭を組み合わせるWIN5投票法を1×4(One by Four)投票法と命名し、今後当サイトで実証的に投票を行い、結果を報告することとする。









