- 2022-12-9

WIN5の収益性:「本命バイアス」を利用した買い方は有効か?
前回で「本命バイアス」は、単勝オッズが低い領域において存在していることが確認できたが、その「偏りを利用してWIN5で収益を上げる方法は存在するのか?」を検証する。
唯一の1番人気馬5連勝は意外な結果?
以下の表は、唯一単勝1番人気が5連勝した時のWIN5成績である。ここで「単勝比率」は単勝オッズから導かれる単勝馬券売り上げの比率で、「WIN5比率」は勝馬を指定したWIN5馬券の比率をレース前後の残り票数の比から求めたもの。「効率」は、「WIN5比率」を「単勝比率」で割った値で高いほどWIN5で多く売れていることを表し、1を超えていれば「本命バイアス」とみなすことができる。
| Leg | 単勝人気 | 単勝オッズ | 単勝比率 | レース前残り票数 | レース後残り票数 | WIN5比率 | 効率 |
| 1 | 1 | 1.9 | 42.11 | 6406292 | 2312392 | 36.1 | 0.86 |
| 2 | 1 | 2.0 | 40 | 2312392 | 903243 | 39.06 | 0.98 |
| 3 | 1 | 3.0 | 26.67 | 903243 | 266695 | 29.53 | 1.11 |
| 4 | 1 | 1.8 | 44.44 | 266695 | 163014 | 61.12 | 1.38 |
| 5 | 1 | 3.4 | 23.53 | 163014 | 43675 | 26.79 | 1.14 |
ここで注目すべきは第1レッグと第2レッグで「効率」がともに1を下回っている点である。これは「本命バイアス」を否定するものであるが、第3レッグ以降は「本命バイアス」が成立している。特に単勝オッズが3倍台の第3レッグと第5レッグで成立していることから、「本命バイアス」とは単純にオッズが低いから偏りが出やすいというものではないようだ。
簡単に取れそうな1500倍・・・?
もう少し調べる必要があるようなので、次に1番人気馬が4勝して、残りのレッグを5番人気馬が勝った2015年10月4日の記録を見てみよう。
| Leg | 単勝人気 | 単勝オッズ | 単勝比率 | レース前残り票数 | レース後残り票数 | WIN5比率 | 効率 |
| 1 | 1 | 2.8 | 28.57 | 5831642 | 1451480 | 24.89 | 0.87 |
| 2 | 1 | 3.2 | 25 | 1451480 | 394534 | 27.18 | 1.09 |
| 3 | 5 | 7.7 | 10.39 | 394534 | 32453 | 8.23 | 0.79 |
| 4 | 1 | 2.5 | 32 | 32453 | 12840 | 39.56 | 1.24 |
| 5 | 1 | 4.4 | 18.18 | 12840 | 2619 | 20.4 | 1.12 |
ケース1と同様にレッグ1では効率が1を割っているが、5番人気馬が勝ったレッグ3を除き、それ以外のレッグでは「本命バイアス」が成立している。ちなみにこの回のWIN5払戻は155,860円で、第3レッグの5番人気馬を選定できれば他のレッグは全て1番人気馬を選定して1500倍以上の配当なので「おいしい馬券」といえるだろう。(ここでいう「おいしい」とは、割と簡単に取れそうなのに配当が高い状態をいうスラングで、感覚的なものなので計数的な裏付けはない場合が多い)
「逆本命バイアス」が配当133万円を演出!
「本命バイアス」が成立していても配当的に「おいしく」なるということはどういうことなのか?どうやらこの辺をさらに詳しく見てみる必要がありそうだ。というわけで、第3のケースはちょっと高配当の2017年3月5日の記録を調べる。
| Leg | 単勝人気 | 単勝オッズ | 単勝比率 | レース前残り票数 | レース後残り票数 | WIN5比率 | 効率 |
| 1 | 3 | 8.3 | 9.64 | 6442437 | 641971 | 9.96 | 1.03 |
| 2 | 4 | 12.8 | 6.25 | 641971 | 41158 | 6.41 | 1.03 |
| 3 | 2 | 4.6 | 17.39 | 41158 | 6690 | 16.25 | 0.93 |
| 4 | 1 | 2.5 | 32 | 6690 | 1586 | 23.71 | 0.74 |
| 5 | 1 | 3.3 | 24.24 | 1586 | 339 | 21.37 | 0.88 |
このケース3のWIN5配当金は1,330,290円で、4番人気以下の組み合わせで1番人気馬も2勝しているのに異例の高配当となった。その原因は、レッグ4とレッグ5の1番人気の勝馬の「効率」が大きく1を下回っていたことで、いわば「逆本命バイアス」というべき事象である。
ここまでの検討で「本命バイアス」は存在しているものの相当に偶然性に左右されることがハッキリした。特に、残り票数が少ないレッグの後半では1番人気馬でも「効率」にばらつきが出やすくなることはこのケース3からも明らかだろう。
3億の悲劇・・・衝撃のグランアレグリア!
次のケースは、極端な「逆本命バイアス」で衝撃的な結末を迎えた2021年5月16日の記録である。
| Leg | 単勝人気 | 単勝オッズ | 単勝比率 | レース前残り票数 | レース後残り票数 | WIN5比率 | 効率 |
| 1 | 16 | 113.5 | 0.7 | 8740324 | 48144 | 0.55 | 0.78 |
| 2 | 6 | 16.9 | 4.73 | 48144 | 1903 | 3.95 | 0.84 |
| 3 | 5 | 12.9 | 6.2 | 1903 | 116 | 6.1 | 0.98 |
| 4 | 7 | 16.6 | 4.82 | 116 | 9 | 7.76 | 1.61 |
| 5 | 1 | 1.3 | 61.54 | 9 | 2 | 22.22 | 0.36 |
この日は、第1レッグから単勝万馬券でその後も10倍以上の単勝配当が続き、最終レッグ前の残り票数は9票。最終レッグの勝馬は単勝1.3倍の大本命馬グランアレグリア。ところが9票中的中は2票でWIN5配当金は、305,911,340円となった。この最終レッグの勝馬の「効率」0.36は1番人気馬としては史上最低の値で、この極端な「逆本命バイアス」のせいで9票中7票が外すという衝撃の結末を迎えた。
なぜ悲劇は起こったか?
まず考えられるのは、ランダム投票である。第1レッグで16番人気馬を選択し、その後も高配当馬が続いているので人為的に選択する難易度は高く、機械にお任せで投票したとすれば最終レッグで1.3倍の大本命を選ばないのもうなづける。この日の第1レッグは18頭立て、以後13頭、14頭、16頭で最終レッグのヴィクトリアマイルが18頭立てだった。したがって、全ての組み合わせは943,488通りになる。全売上8,740,324票のうちランダム投票の割合はわからないが仮に10%程度あったとしても確率的には的中票は1、2票程度であろう。
「大穴バイアス」が導くもの
次の可能性は、いわゆる「大穴バイアス」である。これは配当の高さに目がくらみ、低人気馬を買ってしまう現象で、以下に実際のデータで「大穴バイアス」の存在を明らかにする。
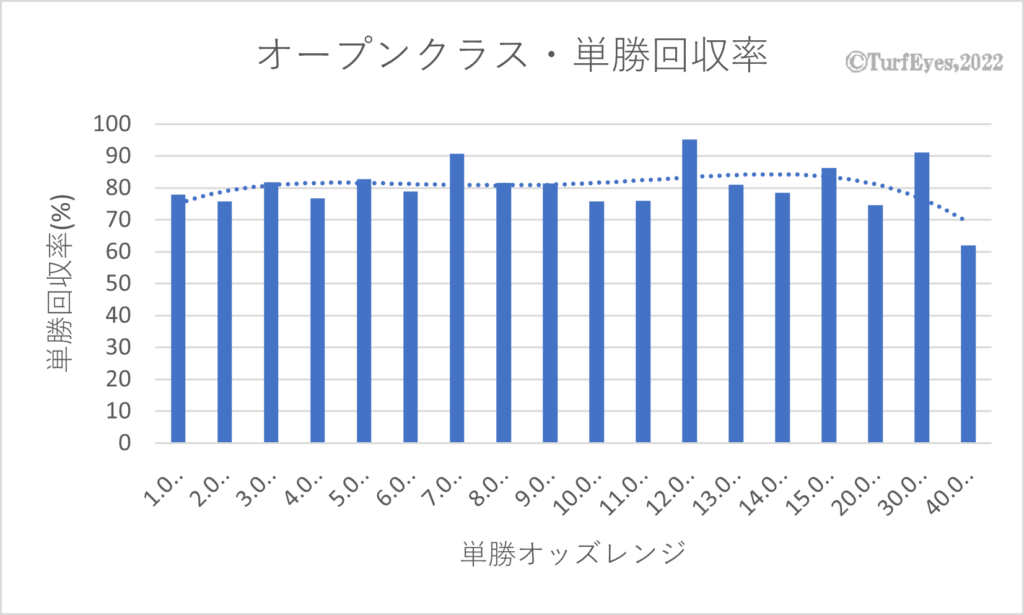
2011年から2022年までのオープンクラス競走約2,900レースの単勝回収率を単勝オッズレンジ毎に集計したグラフ。
40倍以上のレンジの回収率が6割前後に落ち込んでいることが「大穴バイアス」による過剰投票の存在を証明している。
低人気馬が絡むと配当が跳ね上がるWIN5においては「大穴バイアス」は単勝以上に強いことが想像できる。実際にケース4の例では、第1レッグ朱雀Sの単勝113.5倍のコロラトゥーレはその前走で同クラスの同距離の特別で0.3秒差の5着だったので狙えなくもない。そこさえ通過できれば第2~第4レッグは穴党ならば選択できる範囲なので、9票中7,8票はそういった穴狙いの戦術で的中してきたと考えて良いだろう。さて最後のグランアレグリアを買うかどうかの選択。穴党の思考は「大穴バイアス」が「逆本命バイアス」を導き、正解を避けてしまった・・・可能性が高い。
鍵を握る「逆本命バイアス」!
このように若いレッグで単勝高配当が出ると、以後の残り票数は「大穴バイアス」が働いているものの割合が増加する。そのため母集団(外れ票も含めた当該レースの全投票:単勝比率に比例した分布)と残り票の人気馬票の分布(「大穴バイアス」により人気馬の比率が下がる)が異なることになり、以後のレッグでは「逆本命バイアス」が働いているように見えることになる。
したがって、若いレッグで1番人気馬が勝っていない場合は、その後のレッグでは「逆本命バイアス」が働きやすい、といえる。ケース3もそう考えると説明が付くだろう。
「本命バイアス」を利用する方法とは「人気馬を買わない」ことになるが、低人気馬の選定は選択肢が多く難易度が高い。反対に「逆本命バイアス」を利用するのは簡単で1番人気馬(2番人気馬でもいいが)を買うだけである。したがって、「逆本命バイアスを如何に利用するか?」を極めることがWIN5勝利への近道といえるのではないだろうか。









